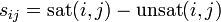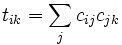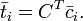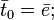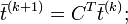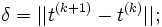EigenTrust Algorithm for Reputation Management

Algorithm

The Eigentrust algorithm is based on the notion of transitive trust: If a peer i trusts any peer j, it would also trust the peers trusted by j. Each peer i calculates the local trust value s_ij for all peers that have provided it with authentic or fake downloads based on the satisfactory or unsatisfactory transactions that it has had. Reputation management

$s_{ij} = \operatorname{sat}(i,j) - \operatorname{unsat}(i,j)$

where sat (i, j) refers to the number of satisfactory responses that peer i has received from peer j, and unsat(i, j) refers to the number of unsatisfactory responses that peer i has received from peer j.

The local value is normalized, to prevent malicious peers from assigning arbitrarily high local trust values to colluding malicious peers and arbitrarily low local trust values to good peers. The normalized local trust value c_ij is then

$c_{ij} = \frac{\max(s_{ij},0)}{\sum_{j} \max(s_{ij}, 0)}$

The local trust values are aggregated at a central location or in a distributed manner to create a trust vector for the whole network. Based on the idea of transitive trust, a peer i would ask other peers it knows to report the trust value of a peer k and weigh responses of these peers by the trust peer i places in them.

$t_{ik} = \sum_{j} c_{ij} c_{jk}$

If we assume that a user knew the c_ij values for the whole network in the form of a matrix C, then trust vector $\bar t_{i}$ that defines the trust value for $t_{ik}$ is given by

$\bar t_{i} = C^T\bar c_{i}.\,$

In the equation shown above, if C is assumed to be aperiodic and strongly connected, powers of the matrix C will converge to a stable value at some point.

$\bar t = (C^T)^x \bar c_{i}. \,$

It seems that for a large value of x, the trust vector $\bar t_{i}$ will converge to the same vector for every peer in the network. The vector $\bar t_{i}$ is known as the left principal eigenvector of the matrix C. We also note that since $\bar t_{i}$ is same for all nodes in the network, it represents the global trust value.

Based on the results above a simple centralized trust value computing algorithm can be written. Note that we assume that all the local trust values for the whole network are available and present in the matrix C. We also note that, if the equation shown above converges, we can replace the initial vector $\bar c_{i}$ by a vector $\bar e$ that is an m-vector representing uniform probability distribution over all m peers. The basic EigenTrust algorithm is shown below: